Informations sur le projet
- Catégorie: Projet scolaire binôme
- Objectif: créer un simulateur avec une interface graphique pour visualiser et tester différentes stratégies sur une grille.
- Date du projet: oct. 2019 - mars 2020
- URL du projet: Plus d'info sur Github
Notions/Concepts/Outils utilisés
- Langages : Python (Tkinter)
- Interface graphique en Python
- Recherche opérationnelle (graphes)
- Diagramme de classes
- Compréhension la problématique
En quoi consiste ce projet ?
Le problème du pompier a été introduit par Bert Hartnell en 1995 lors de la 25e conférence du Manitoba sur les mathématiques et l'informatique combinatoires.
Imaginez qu'à l'instant 0, un incendie se déclare à un sommet d'un graphe G. À chaque instant suivant, le pompier "défend" un sommet de G, puis le feu se propage de chaque sommet "en feu" à tous ses voisins non défendus.
Une fois qu'un sommet est en feu ou défendu, il le reste à partir de ce moment. Le processus se termine lorsque le feu ne peut plus se propager. Un exemple est donné à la figure 1. Dans la forme générale Dans la forme générale du problème, plusieurs incendies peuvent se déclarer, et le ou les incendies sont défendus par un ou plusieurs pompiers.
Une fois qu'un sommet est en feu ou défendu, il le reste. Le processus s'arrête lorsque le feu ne peut plus se propager. Un exemple est donné à la figure 1. Dans la forme générale du problème, plus d'un incendie peut se déclarer, et le ou les incendies sont défendus par un ou plusieurs pompiers.
Ce problème a pour but de sauver le plus grand nombre de sommets.

Ce problème est un problème NP-complet même lorsque le graphe en entrée est un graphe biparti ou un arbre de degré 3.
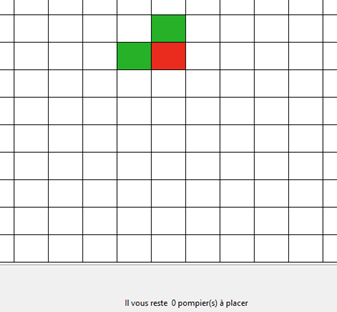
Par conséquent notre projet consiste à créer un simulateur de ce problème en considérant le graphe comme une grille.
Sur cette grille, on commencera à placer un certain nombre de feux puis un nombre de pompiers choisis. Une fois ces pompiers placers on propage le feu (selon un mode choisie) puis l’on répète ces étapes jusqu’à ce que la simulation soit terminée.